Power Equals Work Multiplied By Time.
circlemeld.com
Sep 24, 2025 · 7 min read
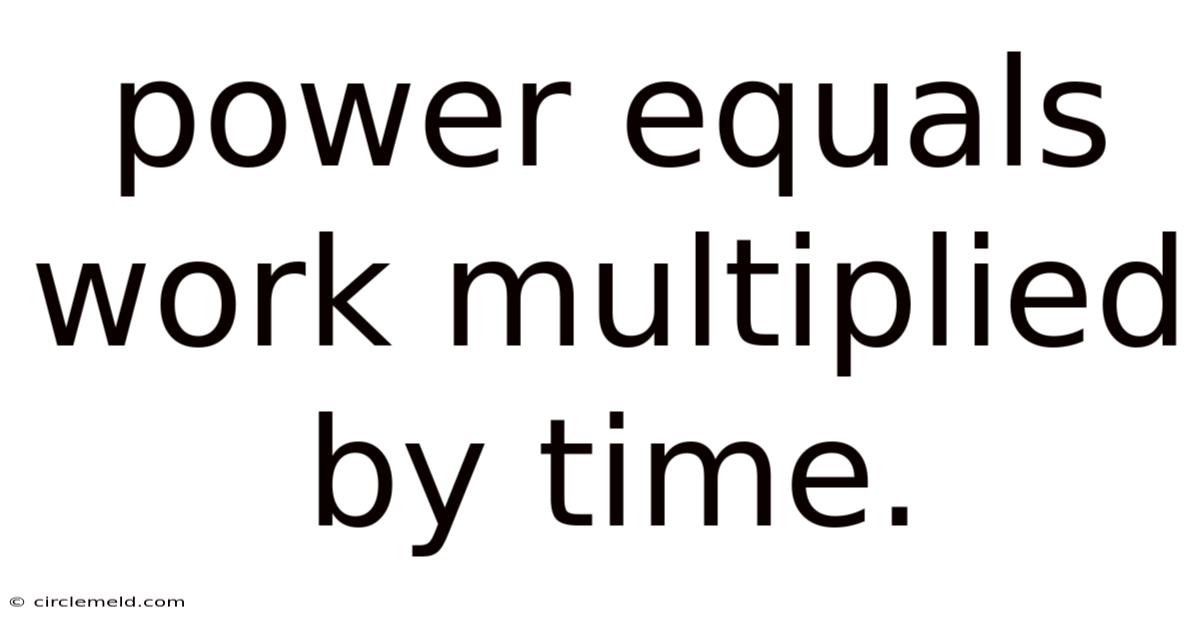
Table of Contents
Power: Unveiling the Relationship Between Work, Time, and Energy
The concept of power is fundamental to our understanding of physics and engineering. While often used colloquially to describe influence or authority, in the scientific realm, power is the rate at which work is done or energy is transferred. Contrary to the often-misunderstood notion that power equals work multiplied by time, the correct formula is actually Power = Work / Time. This article delves deep into the intricacies of this crucial concept, explaining the relationship between power, work, and time, exploring its various applications, and clearing up common misconceptions.
Understanding Work and Energy
Before diving into the definition of power, let's briefly revisit the concepts of work and energy. In physics, work is done when a force causes an object to move a certain distance in the direction of the force. The formula for work is:
Work (W) = Force (F) x Distance (d) x cos(θ)
where θ is the angle between the force and the direction of motion. If the force and displacement are in the same direction, cos(θ) = 1, simplifying the equation to W = Fd.
Energy, on the other hand, is the capacity to do work. It exists in various forms, including kinetic energy (energy of motion), potential energy (stored energy), thermal energy (heat), and many others. The crucial link between work and energy is that doing work always involves a transfer or transformation of energy. When work is done on an object, its energy changes.
Defining Power: The Rate of Energy Transfer
Now, let's define power. Power measures how quickly work is done or energy is transferred. The formula is:
Power (P) = Work (W) / Time (t)
This means that a higher power rating implies that a certain amount of work can be accomplished in a shorter amount of time. The units of power are watts (W), where 1 watt is equal to 1 joule per second (1 J/s). A joule (J) is the SI unit of energy and work.
Exploring the Relationship: Power, Work, and Time
The relationship between power, work, and time is inversely proportional. This means:
-
If the work done remains constant, increasing the time taken to do the work reduces the power. For example, lifting a heavy box slowly requires less power than lifting the same box quickly.
-
If the time taken remains constant, increasing the work done increases the power. Lifting a heavier box in the same amount of time requires more power than lifting a lighter box.
-
If the power remains constant, increasing the work done requires a proportionally longer time. A more powerful engine can complete more work in the same amount of time or complete the same amount of work in a shorter time.
Let's illustrate this with examples:
Example 1:
Imagine two people lifting the same weight (identical work) to the same height. Person A takes 5 seconds, while Person B takes 10 seconds. Person A has a higher power output because they completed the same work in less time.
Example 2:
Consider two cars accelerating to the same speed. Car A, with a more powerful engine, achieves this speed faster than Car B. This means Car A has done the same amount of work (increasing kinetic energy) in less time, resulting in a higher power output.
Example 3:
Suppose a light bulb consumes 100 joules of energy in 1 second. Its power is 100 watts (100 J/1s = 100 W). If it consumes the same 100 joules in 2 seconds, its power is 50 watts (100 J/2s = 50 W). This demonstrates the inverse relationship between power and time when work is constant.
Different Forms of Power
Power manifests in various ways depending on the type of energy being transferred or transformed. Here are some examples:
-
Mechanical Power: This refers to the rate at which mechanical work is done. Examples include the power of an engine, a motor, or a human lifting a weight.
-
Electrical Power: This is the rate at which electrical energy is consumed or generated. It's calculated using the formula P = IV, where I is the current and V is the voltage.
-
Hydraulic Power: This relates to the power transmitted through liquids under pressure, commonly used in hydraulic systems.
-
Thermal Power: This refers to the rate of heat transfer, often expressed in watts.
The Importance of Power in Engineering and Everyday Life
The concept of power is crucial in numerous fields. Engineers use power calculations to design efficient machines, motors, and power systems. In everyday life, we encounter power ratings in various devices, such as light bulbs, appliances, and vehicles. Understanding power helps us choose the right tools for a task, optimizing energy use, and appreciating the interplay between work, time, and energy consumption.
Common Misconceptions about Power
It's essential to address some common misunderstandings surrounding the concept of power:
-
Power is not work multiplied by time: The correct formula is Power = Work / Time. Multiplying work by time doesn't have a physical meaning in this context.
-
High power doesn't always mean high energy: A device can have high power but low energy consumption if it operates for a short period. Conversely, a device can have low power but high energy consumption if it operates for a long period. It's the combination of power and time that determines the total energy consumed.
-
Power is not just about speed: Although speed often correlates with power (faster work implies higher power), power is a more fundamental concept related to the rate of energy transfer, regardless of the specific mechanism.
Calculating Power: A Practical Approach
Calculating power involves determining the work done and the time taken. Here's a step-by-step approach:
-
Identify the work done: Determine the force applied and the distance over which the force acts. Remember to account for the angle between force and displacement.
-
Calculate the work: Use the formula W = Fd (if force and displacement are in the same direction) or W = Fd cos(θ).
-
Measure the time: Accurately measure the time it takes to complete the work.
-
Calculate the power: Divide the work done by the time taken: P = W/t.
Frequently Asked Questions (FAQ)
Q1: What are the different units of power?
A1: The SI unit of power is the watt (W). Other units include horsepower (hp), kilowatts (kW), megawatts (MW), etc.
Q2: How is power related to efficiency?
A2: Efficiency is the ratio of useful work output to the total energy input. High power doesn't necessarily mean high efficiency. A device can have high power but waste a lot of energy in the process, resulting in low efficiency.
Q3: Can power be negative?
A3: In some contexts, like in electrical circuits, power can be negative, indicating energy is being returned to the source (e.g., during regenerative braking in a hybrid vehicle).
Q4: How can I improve the power output of a machine?
A4: This depends on the specific machine but generally involves increasing the force applied, reducing the time taken to do work, or improving the efficiency of the energy conversion process.
Conclusion: Power – A Fundamental Concept in Physics
Understanding the concept of power – as the rate at which work is done or energy is transferred – is crucial for comprehending many physical phenomena and engineering applications. By grasping the relationship between power, work, and time, we gain insights into the efficiency of various systems and the crucial interplay between energy and its rate of usage. While the formula itself is relatively simple, its implications are far-reaching, impacting everything from the design of powerful engines to the efficient operation of everyday appliances. Remember the correct formula: Power = Work / Time, and you'll be well-equipped to tackle the challenges of understanding and utilizing power effectively.
Latest Posts
Latest Posts
-
Rn Critical Alterations In Gas Exchange Assessment
Sep 24, 2025
-
Pn Management Online Practice 2023 B
Sep 24, 2025
-
The Basic Purpose Of Insurance Is To Provide
Sep 24, 2025
-
Using The Problem Solving Approach What Does The B Represent
Sep 24, 2025
-
The Classification Of Stage Iv Of Copd Is Defined As
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Power Equals Work Multiplied By Time. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.