A Number Y Is No More Than
circlemeld.com
Sep 13, 2025 · 6 min read
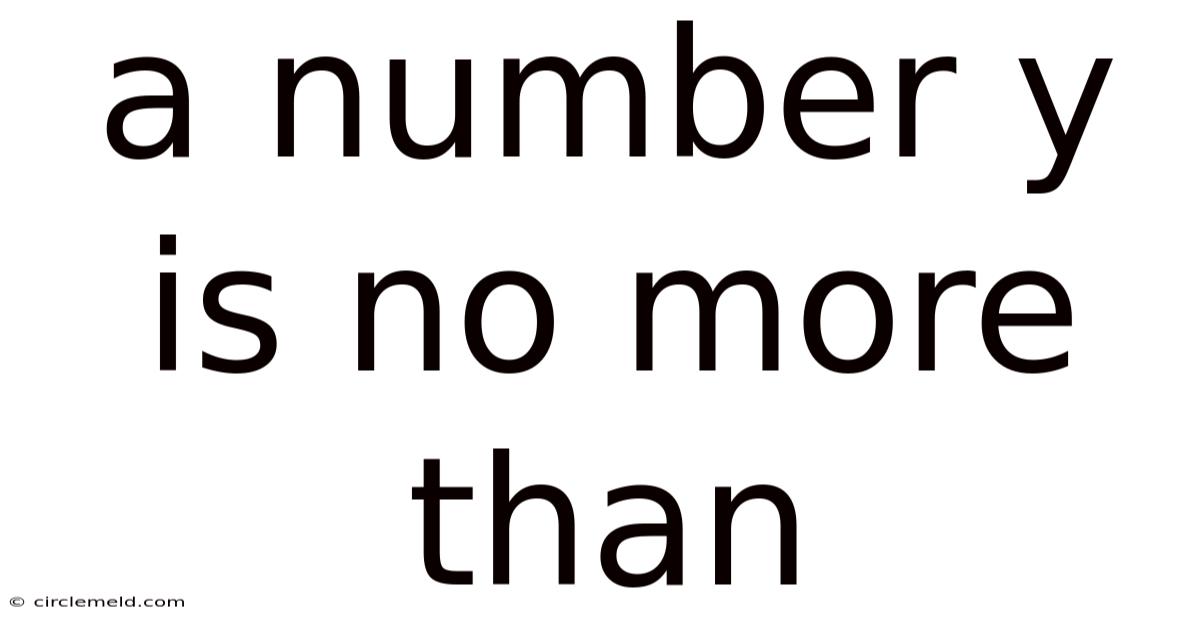
Table of Contents
Understanding "A Number Y is No More Than": Inequalities and Their Applications
The phrase "a number y is no more than" is a common way of expressing a mathematical inequality. Understanding how to translate this phrase and similar ones into mathematical symbols is crucial for solving various problems in algebra, calculus, and real-world applications. This article will delve into the meaning of this inequality, explore different ways to represent it mathematically, and showcase its practical usage through examples. We'll also address common misconceptions and provide a comprehensive FAQ section to solidify your understanding.
What Does "A Number Y is No More Than" Mean?
The statement "a number y is no more than x" signifies that the value of y is less than or equal to the value of x. In simpler terms, y can be equal to x or smaller than x, but it cannot be greater than x. This is a fundamental concept in inequalities, where we compare the relative sizes of two or more quantities. The key is recognizing the words "no more than" imply an upper limit. It's a constraint, defining a maximum possible value for y.
Mathematical Representation:
The inequality "a number y is no more than x" is mathematically represented as:
y ≤ x
The symbol "≤" means "less than or equal to." This notation concisely captures the meaning of the phrase, stating that y's value falls within the range from negative infinity up to and including x.
Examples:
Let's illustrate this with some examples:
-
Example 1: "The temperature (y) is no more than 25 degrees Celsius (x)." This translates to: y ≤ 25°C. This means the temperature can be 25°C or any value lower than 25°C.
-
Example 2: "The number of students (y) in the class is no more than 30 (x)." This translates to: y ≤ 30. This means there can be 30 students or fewer in the class.
-
Example 3: "The cost (y) of the item is no more than $50 (x)." This translates to: y ≤ $50. This signifies that the item's price is capped at $50; it can be $50 or any amount below that.
Solving Inequalities Involving "No More Than":
Solving inequalities involving "no more than" often requires manipulating the inequality to isolate the variable. The rules for manipulating inequalities are similar to those for equations, with one crucial difference: when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality sign.
Example 4:
Let's say we have the inequality: 2y + 5 ≤ 15. To solve for y, we follow these steps:
-
Subtract 5 from both sides: 2y ≤ 10
-
Divide both sides by 2: y ≤ 5
Therefore, the solution to the inequality is y ≤ 5. This means any value of y less than or equal to 5 satisfies the original inequality.
Graphing Inequalities:
Inequalities can be visually represented on a number line. For "y ≤ x," you would graph a closed circle (or a filled-in dot) at the point x on the number line, and shade the region to the left of x, indicating all values less than or equal to x.
Real-World Applications:
The concept of "no more than" appears frequently in real-world situations:
-
Budgeting: "My spending (y) on groceries this week is no more than $100 (x)." This helps you set a spending limit.
-
Weight Limits: "The maximum weight (y) this elevator can carry is no more than 1000 kg (x)." This ensures safety.
-
Speed Limits: "The speed (y) of the vehicle should be no more than 60 mph (x)." This is a crucial safety regulation.
-
Manufacturing: "The number of defective items (y) produced in a batch should be no more than 5% (x) of the total." This is a quality control measure.
-
Engineering: In structural engineering, load-bearing capacities are often expressed as "no more than" values.
Distinguishing "No More Than" from Other Phrases:
It's crucial to distinguish "no more than" from other phrases that might seem similar:
-
"Less than": "y < x" means y is strictly less than x; y cannot be equal to x.
-
"At most": "At most" is synonymous with "no more than." Both indicate an upper limit.
-
"Maximum": "The maximum value of y is x" also implies y ≤ x.
Understanding these subtle differences is vital for accurately interpreting and solving problems.
Common Misconceptions:
A common misconception involves confusing "no more than" with "no less than." "No less than" signifies a minimum value, represented by "≥" (greater than or equal to). Remember to carefully read and interpret the wording of the problem to ensure you use the correct inequality symbol.
Advanced Applications:
The concept extends to more complex scenarios, including systems of inequalities and inequalities involving multiple variables. These are often encountered in optimization problems (finding the best solution within given constraints) and linear programming.
FAQ:
Q1: What happens if the inequality involves a negative number?
A1: The same rules apply. For example, if you have -2y ≤ 6, you would divide both sides by -2 and reverse the inequality sign: y ≥ -3.
Q2: How do I represent "y is no more than 10 and no less than 5"?
A2: This is a compound inequality, represented as: 5 ≤ y ≤ 10. This means y is greater than or equal to 5 and less than or equal to 10.
Q3: Can I use a calculator to solve inequalities?
A3: Many scientific calculators can handle inequalities. However, it's important to understand the underlying principles and to check your answer manually, particularly when dealing with negative numbers or complex inequalities.
Q4: What if the inequality involves variables on both sides?
A4: You still follow the same principles of manipulating the inequality to isolate the variable. You might need to add or subtract terms from both sides to group similar terms together before dividing or multiplying.
Q5: Are there online tools to help solve inequalities?
A5: Yes, many online calculators and math solvers can handle inequalities, offering step-by-step solutions to help you understand the process. However, understanding the manual process is crucial for developing your problem-solving skills.
Conclusion:
Understanding the meaning and application of "a number y is no more than x" is fundamental to mastering inequalities. This seemingly simple phrase opens doors to solving a wide array of mathematical problems and real-world challenges. By mastering the mathematical representation (y ≤ x), the techniques for solving inequalities, and the ability to distinguish it from similar phrases, you'll develop a strong foundation in mathematical reasoning and problem-solving. Remember to practice regularly to solidify your understanding and build confidence in tackling more complex inequalities in the future.
Latest Posts
Latest Posts
-
Tendency To Perceive A Complete Figure Even If Gaps Exist
Sep 13, 2025
-
3 Reasons For The Founding Of The Georgia Colony
Sep 13, 2025
-
A Bag Mask Device Is Used To Provide
Sep 13, 2025
-
Two Sources Of Energy That Generally Have Limited Environmental Impacts
Sep 13, 2025
-
Periodic Table With Element Names And Symbols
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about A Number Y Is No More Than . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.